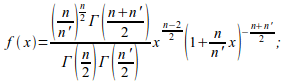
Для начала хочется вспомнить знаменитое в 19-м веке высказывание фон Тюнена:
Вот почему авторы посчитали необходимым поделиться с этими двумя группами "горе экономистов" своими методиками, постановкой задач и конкретными алгоритмами.
Предложенная авторами методика расчета рисков на основе нейронных моделей может эффективно применяться для оценки деятельности любых хозяйствующих субъектов, а не только для финансовых учреждений типа банк.
Давайте ответим на простой вопрос какова Цель нашего исследования, или проще для чего мы все это делаем?
И на самом деле существуют мощнейшие Центробанки, Минфины развитых стран, в том числе США, рейтинговые, аналитические, аудиторские компании, экономические ВУЗы мирового уровня. Они формируют, владеют, имеют доступ к огромным базам на всех микро, мезо, макро уровнях экономики - воистину с бесконечным количеством данных, вооружены самыми совершенными теориями и методиками, а результат смешной - регулярно пропускали, пропускают, и будут пропускать все кризисы.
Обратите внимание: все кризисы ими были пропущены, поэтому и были для них неожиданными.
Почему образуется такой воистину забавный парадокс - какой-то малочисленный коллектив исследователей знает все, имея ограниченный доступ к информации, а другие, имея неограниченные ресурсы, не знают ничего и регулярно с удивительным упорством и болезненной настойчивостью делают очевидные ошибки.
Поэтому все то, что приводится ниже, является аксиомами методики авторов:
Попытаемся разобраться с этими "сложнейшими" для многих экономистов расчетами, и что, самое главное, попытаемся получить результаты, которые многим недоступны и/или просто не грезились.
Итак, займемся этими элементами методики авторов, которых строятся на трех шаговом алгоритме.
Вернемся еще раз к цели нашей работы: необходимо дать оценку рисков банка, через оценку рисков их клиентов и/или их отраслевых групп. Данный подход очевиден — именно клиенты определяют устойчивость, риски банка, а не наоборот, конечно, при условии профессионализма персонала банка. К сожалению, у банкиров это достаточно редкое явление. Последний кризис 2008-2010 г.г. это очередной раз доказал. Это результат непонимания банками того факта, что клиенты формируют доходы банка, а не наоборот. Предложенная в работе методика убедительно, подчеркнем, на цифрах, моделях, а не на основе виртуальных концепций, это доказывает.
Приведем пример для построения моделей рисков, эффективности....
Если объемы продаж, и, как следствие, платежи клиентов банка будут падать, то это губительно отразится на депозитном и кредитном портфеле банка, на снижении эффективности банковских операций, а далее до рисков рукой подать. Таким образом, рассчитав риски клиентов, практически определяется депозитный, кредитный портфельный риск банка. Алгоритм опирается на обязательные обширные исследования публичной отчетности фирм обслуживающихся в том или ином банке, которые обязаны проводить его аналитические службы. После чего аналитики по данным исследованной публичной отчетности фирм той или иной отрасли на основании экспертных оценок обязаны определить:
Представленный алгоритм практически не обращает никакого внимания на тот факт, что исходные данные как бы статистически размыты. Алгоритм совершенно не интересует факт размытости, при любых вариантах он все равно проведет среднюю эталонную линию, для исследуемого i-го фактора для каждого предприятия той или иной отрасли.
В основу методик авторов положены базовые идеи теории размытых множеств, пространств, хаоса и нейронных сетей. Этот авторский подход принципиально отличается от классической статистики и ее приложения эконометрики. При этом авторами активным образом используется наработанный инструментарий, при условии, что он не противоречит идеологическому вектору теории размытых множеств, пространств, хаоса и нейронных сетей. Конечно, должно соблюдаться еще одно самое важное условие – если метод прост для понимания, то и алгоритм можно описать на раз, два, три шага. Вот почему материал целенаправленно излагается на уровне знаний не выше 7-го класса школы. При этом результат авторских методик, моделей превосходит по эффективности всю сложность, запутанность в изложении классических эконометрических подходов. Главное в авторских подходах, максимально быстро и просто достигнуть поставленной цели, позволяет дать объективную оценку рисков банка, а это, возможно, только через оценку рисков их клиентов и их отраслевых групп, но не наоборот, как того требуют Центральные Банки развитых стран. Эффективность их методик должна определять реальная экономика.
Далее с помощью регрессионного, кластерного, дискриминантного анализа аналитические службы банка с помощью предлагаемой системы определяют потенциалы и риски депозитного и кредитного портфелей и риски ликвидности банка. Практически банком сначала определяются риски каждого предприятия индивидуально, которые далее и трансформируются в риски банка и риски его депозитного и кредитного портфеля.
Логика проста, если риски у предприятия, которое является клиентом банка, низкие, то при любых потрясениях на рынке предприятия его денежные потоки через банк будут подвержены незначительному снижению и наоборот.
Таким образом, контролируя и оценивая денежные потоки предприятия, аналитические службы банка и определяют свои риски и далее потенциальные ежедневные остатки на банковских счетах этого предприятия. Вариация, потенциальное, прогнозируемое колебание ежедневных остатков на банковских счетах каждого предприятия и будет определять суммарный, интегральный ежедневный денежный потенциал депозитного портфеля банка. В свою очередь интегральный ежедневный денежный потенциал депозитного портфеля банка будет формировать ежедневный денежный потенциал кредитного портфеля банка.
Сначала Энрико Ферми в 1930-х годах в Италии, а затем Джон фон Нейман и Станислав Улам в 1940-х в Лос-Аламосе (ядерный центр в США) предположили использовать связь между стохастическими процессами и дифференциальными уравнениями "в обратную сторону". Они предложили использовать стохастический подход для аппроксимации многомерных интегралов в уравнениях переноса, возникших в связи с задачей о движении нейтрона в изотропной среде.
Идея была развита Уламом, который, по иронии судьбы, также как и Фокс боролся с вынужденным бездельем во время выздоровления после болезни, и, раскладывая пасьянсы, задался вопросом, какова вероятность того, что пасьянс "сложится". Ему в голову пришла идея, что вместо того, чтобы использовать обычные для подобных задач соображения комбинаторики, можно просто поставить "эксперимент" большое число раз и, таким образом, подсчитав число удачных исходов, оценить их вероятность. Он же предложил использовать компьютеры для расчётов методом Монте-Карло.
Появление первых электронных компьютеров, которые могли с большой скоростью генерировать псевдослучайные числа, резко расширило круг задач, для решения которых стохастический подход оказался более эффективным, чем другие математические методы. После этого произошёл большой прорыв и метод Монте-Карло применялся во многих задачах, однако его использование не всегда было оправдано из-за большого количества вычислений, необходимых для получения ответа с заданной точностью.
Годом рождения метода Монте-Карло считается 1949 год, когда в свет выходит статья Метрополиса и Улама "Метод Монте-Карло". Название метода происходит от названия города в княжестве Монако, широко известного своими многочисленными казино, поскольку именно рулетка является одним из самых широко известных генераторов случайных чисел. Станислав Улам пишет об этом в своей автобиографии "Приключения математика". Название было предложено Николасом Метрополисом в честь его дяди, который был азартным игроком.
Идея метода Монте-Карло опирается на тот факт, что экономист в своей повседневной деятельности вынужден исследовать практически бесконечное множество процессов реальной экономики. И что, самое важное, - все эти процессы исключительно индивидуальны, и, как следствие, определяются своими оригинальными статистическими функциями распределения.
В тоже время классическая статистика может предложить экономисту лишь десяток классических вероятностных функций распределения и их интегралов вероятности. Очевидно, что с помощью этого весьма ограниченного множества классических вероятностных функций распределения, невозможно описать бесконечное множество процессов, происходящих в реальной экономике. Практически экономист после исследования того или иного фактора и напряженного сбора статистической базы вынужден затрачивать огромное количество времени не на описание, моделирование конкретного исследования, а на откровенную подгонку, искажение процессов реальной экономики под одну из десяти классических статистических вероятностных моделей и их производных. Понятно, что полученные модели ничего общего не имеют с исследуемыми экономическими проблемами. В результате уже на первом этапе обработки статистических данных экономист вынужден сознательно закладывать ошибки и искажения. Последствия такого подхода вполне очевидны.
Мало того, экономист должен не хуже математика разбираться в этих сложнейших многоярусных интегральных вероятностных моделях, кроме этого, знать и помнить все их особенности по применению и, что особенно важно, досконально знать и разбираться в ограничениях применяемых моделей.
Приведем пример только одной из классической статистической функции из известных пар десятков функций. f(x) - плотность распределения случайной величины по закону Фишера, вычисляется по формуле:
В ней Г(z) – гамма-функция, или интеграл Эйлера, который можно представить в следующем виде:
В свою очередь Гамма-функция может быть описана с помощью формулы Эйлера:
Разобраться в данной модели даже для математиков достаточно трудная задача, если вспомнить еще и о многообразии ограничений, которые также описываются или функциями, или функционалами. Ведь любое ограничение требует сложнейших решений по трансформации и подгонке этих многоярусных интегральных моделей под конкретный экономический процесс.
Поэтому метод Монте-Карло и призван решить проблемы классической статистики и не забивать голову экономисту лишней сложнейшей даже для математиков информацией. И, самое главное, объективно просто можно мгновенно описывать экономическую среду практически простым нажатием клавиши.
Метод Монте-Карло в состоянии моделировать бесконечное множество любых процессов реальной экономики на основании не абстрактных десяти статистических моделей с массой ограничений, а моделей полностью соответствующих собранным экономистом статистических данных того или иного экономического фактора и/или переменной, и/или процесса.
При классическом методе экономисту необходимо реализовать следующий алгоритм:
В методе Монте-Карло данный алгоритм обработки данных просто исключается, как следствие трудовые затраты, финансирование, время этого этапа по сравнению с классическим методом равны нулю. В результате точность, скорость обработки многократно превосходит классический метод. Мало того, тестовые сравнительные испытания авторов показали, что при генерировании выборки десятка классических вероятностных функций распределения и их интегралов вероятности алгоритм метода Монте-Карло работает значительно быстрее.
Ниже приведен пример статистического генератора.
Когда получена экспериментальная выборка того или иного случайного процесса, естественно возникает желание, а чаще практическая потребность описать ее вероятностную функцию распределения и многократно ее повторять в дальнейшем для каких-либо экспериментов.
Рассмотрим пример, допустим, есть нормальная функция плотности распределения или любая другая нестандартная функция плотности распределения.
По ней несложно построить интеграл вероятности – достаточно вспомнить, что любой интеграл – это сумма всех элементов функции плотности распределения, которые перед суммированием необходимо нормировать, т.е. разделить величину каждого элемента гистограммы на сумму величин всех элементов гистограммы. Кстати, дифференцирование - это не что иное, как вычитание.
Пусть некоторому экономисту необходимо исследовать цены на конкретный товар, продукцию, услугу на некотором региональном, отраслевом рынке:
Эти расчеты и результирующий график показаны в табл. 1.2.
Таблица 1.2.
Таблица 1.3.
Естественно, на следующем этапе возникают очень простые вопросы:
На эти простые вопросы и необходимо дать очень конкретные ответы.
Начнем рассматривать предлагаемую методику с ответа на первый вопрос.
Это нестандартные функции распределения, стандартные функции в методике авторов полностью исключаются из рассмотрения раз и навсегда. Методика не предлагает, а требует никогда не использовать классические стандартные функции распределения и их интегралы вероятности.
Рассмотрим ответы на последние два вопроса.
Чтобы исключить неточности, связанные с тем, что между точками интеграл вероятности описывается прямыми, а не кривыми необходимо с помощью сплайн функции аппроксимировать полученный интеграл вероятности.
Преимущество сплайн функций по сравнению с полиномом только в одном: с ростом экспериментальных данных получаемый интеграл вероятностей по гистограмме плотности распределения может оказаться больше чем 70-80 точек по количеству отсчетов. При этом и большем объеме точек полином переходит в состояние возбуждения, т.е. генерирует повышенные ошибки. Сплайн функции, несмотря на меньшую точность, лишены этих недостатков – они устойчиво работают с большим количеством точек. Кроме этого, учитывая, что функция плотности вероятности это монотонно растущая функция (без выбросов см. рисунок), как следствие сплайн функции неплохо аппроксимирует любую выборку, кроме одного ограничения.
Разница значений аргументов соседних точек Xi+1 & Xi должны быть не равны 0, т.е.
D=X(i+1) - X(i)<>0.
В противном случае происходит сбой в расчете коэффициентов сплайна:
E=∆Y/∆X=(Y(i+1)-Y(i))/D,
т.к. величина первых разностей или дифференциал функции:
∆X=D=X(i+1)-X(i)<>0
находится в знаменателе, а деление на 0 вызовет очевидный сбой.
Тем не менее, данный момент программа сплайн функций отрабатывает, так как сознательно вводится погрешность в разницу значений аргументов соседних точек:
D=X(i+1)-X(i)=0.0000001,
хотя точность коэффициентов сплайна снижается. В программе это решено следующим образом:
D = X(i+1) — X(i) ' Вычитание или Приращение, т.е. дифференциал
If D = 0 Then D = 0.0000001 ' Если знаменатель = 0, то назначить Малую Величину
….
E = (Y(i+1) - Y(i)) / D ' Вычитание или Приращение, т.е. дифференциал
В целом благодаря тому, что интегральная функция плотности вероятности это монотонно растущая функция (без существенных выбросов), как следствие сплайн функция неплохо аппроксимирует любую выборку.
Когда с помощью сплайн функции вычислен интеграл вероятности, можно приступать к процессу моделирования с помощью метода Монте-Карло, как это показано на рисунке.
Генератор функции равномерного распределения Rnd(), как известно, генерирует псевдослучайные числа в диапазоне (0-1). Для нас это значения интегральной функции, изменяемой от 0% до 100%, т.е. В диапазоне (0-1).
Например, как показано на рис. 1.18. это Y1 & Y2, и далее необходимо определить соответствующие значения Х1 & Х2, т.е. осуществить обратное преобразование – по известным значениям функции интеграла вероятности Y1…Yn искать неизвестные значения аргументов распределения Х1…Хn. Когда аргументы распределения Х1…Хn получены – это и есть функция распределения, вид и значения которой не были известны.
Рис. 1.18. Моделирование функции распределения с помощью метода Монте-Карло
В нашем случае на рис. 1.18. это нормальное распределение (колокольчик) – весьма редкое явление экономике, но и оно легко моделируется. При этом экономисту нет необходимости утруждать себя запоминанием сложных зависимостей типа:
В экономике видов распределений практически бесконечно, а с помощью метода Монте-Карло можно это бесконечное множество функций распределений и построить.
Перед процессом генерации все сплайн коэффициенты были вычислены с помощью функции:
SplineC(X, F, C)
где F – массив значений функции Y от Х, т.е. Y=F(X)
Х - массив значений Х,
С - массив значений сплайн коэффициентов.
В результате, используя обратное преобразование – вместо Х ставим значение Y, а вместо Y ставим значение Х, на место аргумента Xi ставим генератор Rnd(), то на выходе сплайн функции мы получим очередное случайное значения Хi:
Х(i) = SplineP(F, X, C, Rnd()), обратное преобразование.
Сравните с прямым преобразованием, когда по Х формируются значения функции F=Y(i), а на место значения Rnd() ставим значение Xi.
Y(i) = SplineP(X, F, C, Х(i)), прямое преобразование
где F – массив значений функции Y от Х,
Х - массив значений Х,
С - массив значений сплайн коэффициентов,
Rnd() – генератор случайных значений Yi.
i – текущий индекс значения генерируемого массива i=1...N, где N размер генерируемой выборки.
В результате по данным Y1,Y2,…,Yi, как показано на рисунке ранее, будут получены соответствующие значения Х1,Х2,…,Xi. Генерация случайных значений Х1,Х2,…,Xi заканчивается, когда полностью сформирована выборка, т.е. i=N.
Отметим еще ряд дополнительных ограничений. Любая экспериментальная выборка может обладать так называемыми тяжелыми хвостами, которые образуются в результате физических, социальных, экономических свойств исследуемых объектов.
Например, при исследовании эконометрической модели продолжительности жизни для актуарных расчетов по страхованию жизни исследователь непременно сталкивается с проблемой повышенной смертности в момент рождения, т.е. в "0" год жизни, как это наглядно показано на рис. 1.19. - мы видим достаточно сильный выброс (т.н. тяжелый хвост) смертности в грудном “0” возрасте и в «100» летнем возрасте.
Рис. 1.19. Тяжелые хвосты или выбросы в плотности распределения, и естественные смещения в интеграле вероятности — в «0» возрасте интеграл вероятностей больше 0%, а должно быть равно 0%, при «100» летнем возрасте интеграл вероятностей меньше 100%, а должно быть равно 100%. Статистика по дожитию.
В результате интегральная вероятностная модель при Х1=0 будет принимать не нулевые значения, т.е. F(Х1)<>0%. В этом случае образуется так называемый тяжелый хвост – выброс, а интегральная функция вероятности в различные временные периоды будет принимать значения в диапазоне F(Х1)=1,7-2,4%, что также наглядно видно на графике. Т.е. интегральная функция вероятности при Х1=0 не будет равна нулю F(Х1)>0. В рассматриваемом примере F(Х1)=1,7-2,4%.
Как следствие при аппроксимации данной функции с помощью сплайн функций Х(i)=SplineP(F, X, C, Rnd()) в связи с тем, что сплайн вытягивает F(Х1) в отрицательную зону Х1, при генерации будет образовываться хвост с отрицательным возрастом Х(i)<Min(Xi)<0 лет. Понятно, что человек в реальной жизни не может иметь возраст равный минус десять или минус пять лет. Это искажение реальной картины формируется исключительно сплайн функцией. Такая же ситуация может возникать, когда в статистическом учете фиксируется условная максимальная продолжительность жизни человека не более 100 лет, т.е. Х(i)<Max(Xi)<100 лет. Это также наглядно показано на графике - мы видим не очень сильный всплеск в "100" лет, в сравнении с "0" годом, но и это тоже выброс или тяжелый хвост.
Данный момент логично вытекает из того, что вероятность случайной величины ξ окажется в интервале a'=Min(ξ), b'=Max(ξ), равна интегралу
Или с учетом минимаксных ограничений данный интеграл можно записать в виде:
И далее чтобы разыгрывать случайные значения ξ необходимо составить уравнение:
Заметим, что функция плотности вероятности р(х) описывается в виде аппроксимирующей сплайн функции, генерируемой программой. Т.е. мы практически не нуждаемся в знании, каким образом ее можно представить математически, или какую выбрать стандартную функцию распределения. Нас больше интересует экономический смысл, а не собственно функция и ее математическая форма и выражение. Нас интересует конкретные значения функции вероятностей F(Xi) и значений аргумента Xi и/или наоборот.
Таким образом, для исключения невозможных ситуаций, характерных для физических, социальных, экономических свойств исследуемых объектов, нам в программный код модели генератора необходимо ввести эти минимаксные ограничения, как слева, так и справа по генерируемой выборке по критерию Min(Xi) & Max(Xi). В результате программная итерационная модель генератора должна быть расширена следующим кодом ограничений:
'
Arg(i)=SplineP(F, X, C, Rnd()) 'Обратное преобразование.
If Arg(i) < MinXi Then Arg(i)=MinXi 'Ограничение по MinXi
If Arg(i) > MaxXi Then Arg(i)=MaxXi 'Ограничение по MaxXi
'
В целом весь процесс генерации модели можно легко представить в виде более чем простого программного модуля:
ReDim X(1 To N) As Double 'Массив => Xi
ReDim F(1 To N) As Double 'Массив => Y=F(Xi)
ReDim C(1 To N) As Double 'Массив => C => К-тов сплайнов
ReDim Arg(1 To N) As Double 'Массив => Arg => массив случайных чисел Х(i), по данным функции Y=F(X)
'
On Error Resume Next ' Отключает обработчик ошибки
'
'Ввод ограничений для генератора случайных чисел по критерию Min(Xi) & Max(Xi).
'
MinXi= минимальное возможное значение Xi
MaxXi= максимальное возможное значение Xi
'
'Ввод массива данных Х & Y=F(X)
Call InArr(X, F)
'Вычисление к-тов сплайна C для массива данных Х & Y=F(X)
Call SplineC(X, F, C)
'Генерация массива случайных чисел Х(i), по данным функции Y=F(X)
For i=1 to N
Arg(i)=SplineP(F, X, C, Rnd()) ' Генерация массива аргументов Arg(i)
' ОБРАТНОЕ преобразование. По значению Yi (в формуле Arg) вычисляем Xi
' Сравните с прямым преобразованием, когда по Х формируются значения функции F=Y(i), а на место значения Rnd() ставим значение Xi.
' Y(i) => SplineP(X, F, C, Х(i)), прямое преобразование
' Следующий оператор формирует ОГРАНИЧЕНИЯ по Min&Max
'
If Arg(i) < MinXi Then Arg(i)=MinXi 'Ограничение по MinXi
If Arg(i) > MaxXi Then Arg(i)=MaxXi 'Ограничение по MaxXi
'
Next i
'
Как видно из приведенного модуля, метод Монте-Карло очень легко реализуется практически тремя строками программы.
'Генерация массива случайных чисел Х(i), по данным функции интеграла вероятностей Y=F(X)
For i=1 to N
'
Arg(i)=SplineP(F, X, C, Rnd()) ' Генерация по Yi статмассива Хi
If Arg(i) < MinXi Then Arg(i)=MinXi 'Ограничение по MinXi
If Arg(i) > MaxXi Then Arg(i)=MaxXi 'Ограничение по MaxXi
'
Next i
Конечно, при условии, что С - массив значений сплайн коэффициентов предварительно рассчитан.
Рассмотренный алгоритм метода Монте-Карло позволяет генерировать выборочную последовательность для любой экспериментальной функции распределения плотности вероятности. Это особенно важно для экономических исследований. К сожалению, или радости, экономику на 90-95% невозможно описать классическим набором стандартных вероятностных функций распределений. Хотя в среде экономистов все еще преобладают традиции прошлого века, а ведь на дворе наступила эпоха всеобщей компьютеризации.
Мало того, проведенные испытания метода Монте-Карло убедительно показали скоростное превосходство по отношению к стандартным вероятностным функциям распределения. Практически перед экономистами впервые открылась возможность широкого внедрения в эконометрические исследования, моделирования теории размытых множеств, нейронных сетей, вместо того чтобы с удивительным упорством "притягивать за уши" или проще сознательно закладывать ошибки в стандартные вероятностные функции распределения при описании экономических процессов.
Перед тем как построить генератор необходимо:
Рис. 1.20. Простое линейное регрессионное уравнение вида y=kx
И правда, что может быть проще. Допустим, нам необходимо описать линейное уравнение Y=k*X, где k — это угол наклона. При этом необходимо так провести эту линию (регрессионное уравнение), чтобы расстояние от линии до любых точек (статистических данных) было бы минимально. Этого можно добиться, если правильно подобрать угол наклона k, что подтверждается коэффициентом точности, детерминации или корреляции R2 – он близок к "1", когда точки все ближе к построенной линии, как это показано на рисунке. Соответственно, равен "1", когда все статистические данные лежат прямо на линии. Равен "0", когда все статистические данные разбросаны на всей поверхности, и поэтому провести только одну линию невозможно – можно провести лишь их бесконечное множество.
Итак, нам известен вектор Y, состоящий из множества значений yi, допустим этих статистических данных 30, т.е. их количество лежит в диапазоне i=1-30. Также известны все значения вектора X. Практически каждому известному значению хi соответствует его также известное значение yi и так 30 раз, т.е. yi=ki*xi. В этой задачке осталось вычислить неизвестную величину угла наклона – k. Для этого необходимо, как всех учили еще в начальных классах школы, проделать ну очень "сложные" преобразования k=1/x*y=y/x, или в векторной форме - k=1/Х*Y,
Одна сложность вектора Y & X – это массив значений, точек, а угол наклона – k должно быть получено как одно число, а не как массив чисел.
Для того, чтобы решить эту задачу вспомним матричные преобразования. Из матричных вычислений известно, что если преобразовать (транспонировать, повернуть на 90o, или на 1/2) матрицу-колонку вектора X в матрицу-строку – X', и далее перемножить строку X' на колонку X получим X'X, то получим уже не матрицу, вектор множества чисел, а только одно число x. Аналогичные преобразования необходимо сделать и с массивом точек вектора Y, т.е. умножить строку X' на колонку вектора Y, в результате также получим уже не матрицу, вектор множества чисел, а только одно число y.
Запишем эти матричные преобразования.
k = 1/X'Х * X'Y
или можно представить как
k = (X'Х)-1 * X'Y
Практически если сократить числитель и знаменатель на строку X', то будет получено исходное матричное представление k=1/Х*Y=(Х)-1*Y. Так, что нами математически ничего не было нарушено. Зато в результате найден угол наклона – k как одно число, а не массив чисел .
Расширим данную задачу.
Допустим, нам необходимо получить уравнение y=k0+k1*x, как представлено на втором рис. 1.21., т.е. необходимо найти еще свободный коэффициент k0, кроме угла наклона k1.
Рис. 1.21. Простое линейное регрессионное уравнение вида y=k0+k1*x
Удивительно, но и для этой задачи используются те же матричные преобразования вида:
k = (X'Х)-1 * X'Y
Тем не менее, необходимо разобрать один момент. Коэффициент угла наклона k1 привязан к вектору Х (переменным числам). В тоже время свободный коэффициент k0, не привязан ни к какому вектору, а это нарушает условия матричных вычислений. Для устранения этого нарушения - умножим свободный коэффициент k0 на вектор столбец, состоящий из одних единиц, обозначим его как "I". Ничего не изменится от умножения "1" на свободный коэффициент k0, но матричные требования соблюдены .
Для того, чтобы решить и эту вторую задачу опять обратимся к матричным преобразованиям. Преобразуем (транспонируем, повернем на 90о) матрицу-колонку, состоящую из двух векторов I & X в матрицу-строку. Для простоты обозначим эту матрицу, состоящую из двух строк, как – X'. Далее перемножим эту матрицу-строку, состоящую из двух векторов I & X, на матрицу-колонку, состоящую из этих же двух векторов I & X. В результате получим X'X, но уже не матрицу или вектор множества чисел, а квадратную матрицу размером 2х2 (две строки на две колонки) - x'x. Аналогичные преобразования необходимо сделать и с массивом точек вектора Y, т.е. умножить матрицу-строку, состоящую из двух векторов I & X на колонку вектора Y, в результате получим матрицу размером 2х1 - x'y.
Уточним только, что при одном коэффициенте угле наклона - k1 обозначение принималось как число – k. При расчете двух коэффициентов получим уже не число k, а вектор столбец из двух элементов: в первой строке - свободный коэффициент k0, во второй строке - угол наклона k1. Поэтому этот вектор-столбец регрессионных коэффициентов обозначим большой жирной буквой K. Запишем эти матричные преобразования.
K = 1/X'Х * X'Y
или можно представить как
K = (X'Х)-1 * X'Y
Практически если сократить числитель и знаменатель на строку X', то будет получено исходное матричное представление K=1/Х*Y=(Х)-1*Y. Так, что нами ничего не было нарушено. Зато в результате найден вектор-столбец, состоящий из двух элементов:
В первой строке - свободный коэффициент k0.
Во второй строке - угол наклона – k1.
Как видно из приведенных примеров, расчет любого количества регрессионных коэффициентов, многофакторных регрессионных уравнений легко представить в матричном виде:
K = (X'Х)-1 * X'Y
Алгоритм же расчета регрессионных коэффициентов для построения регрессионных, функциональных уравнений любой сложности просто элементарен.
Этот алгоритм можно представить в виде табл. 1.4., где X & Y были представлены как одномерный вектор:
Уточним - каждый из пунктов алгоритма, в свою очередь, должен рассматриваться и описываться своей подсистемой и как следствие - своим индивидуальным алгоритмом.
Итак, эталонная модель нами получена. Как видно из рисунка, она как бы делит плоскость статистических данных по i-фактору на две части. Практически осуществлен классический дискриминантный (классификационный, кластерный) анализ. Логика анализа проста. Рассмотрим его на примере фактора себестоимость рис. 1.22.
Рис. 1.22. Анализ фактора себестоимость. Риск объекта минимален.
Если исследуемое предприятие при реализации некоторого объема продаж имеет себестоимость ниже чем в среднем на рынке, как это показано на графике, то его можно отнести к условно эффективным предприятиям. Подчеркнем только по данному i-му фактору. Это наглядно видно на рис. 1.22.- предприятие (его жирная точка) находится в нижней части плоскости.
Если исследуемое предприятие при реализации некоторого объема продаж имеет себестоимость выше чем в среднем на рынке, как это показано на графике, то его можно отнести к условно неэффективным предприятиям. Подчеркнем только по данному i-му фактору. Это наглядно видно на рис. 1.23. - предприятие (его жирная точка) находится в верхней части плоскости.
Рис. 1.23. Анализ фактора себестоимость. Риск объекта максимален.
Благодаря такой достаточно простой классификации достигается разделение всех предприятий по каждому i-му фактору на две плоскости, области – средне эффективных (часть плоскости ниже линии регрессионного уравнения, включая ее саму) и средне неэффективных предприятий (часть плоскости выше линии). После чего нетрудно перейти от категории эффективности к категории рисков. Понятно, что эффективные предприятия обладают низкими рисками для банка по сравнению с предприятиями, у которых эффективность ниже, в нашем примере предприятия, имеющие более высокую себестоимость.
Практически банком сначала определяются риски каждого предприятия индивидуально, которые далее и трансформируются в риски банка и риски его депозитного и кредитного портфеля. Логика проста, если риски у предприятия, которое является клиентом банка, низкие, то при любых потрясениях на рынке предприятия его денежные потоки через банк будут подвержены незначительному снижению и наоборот. Таким образом, контролируя и оценивая денежные потоки предприятия, аналитические службы банка и определяют свои риски и далее потенциальные ежедневные остатки на банковских счетах этого предприятия. Вариация, потенциальное, прогнозируемое колебание ежедневных остатков на банковских счетах каждого предприятия и будет определять суммарный, интегральный ежедневный денежный потенциал депозитного портфеля банка. В свою очередь интегральный ежедневный денежный потенциал депозитного портфеля банка будет формировать ежедневный денежный потенциал кредитного портфеля банка.
Таким образом, построив регрессионное уравнение эталонной модели, практически решается задача качественной оценки эффективности, рисков для каждого предприятия по каждому i-му фактору. Кроме этого тут же можно дать не только качественный, но количественный анализ и оценку любого исследуемого предприятия по любому i-му фактору. Практически, подставив данные любого предприятия в регрессионное уравнение эталонной модели, можно определить насколько он эффективен/неэффективен в денежном выражении по отношению к средним показателям по исследуемому i-му фактору, который сложился на данном рынке.
Yэф=k*Xi - Yi ,
Если полученный результат больше равно "0", то предприятие эффективно работает в денежном выражении на полученный результат, чем среднее предприятие на данном конкурентном рынке.
Если полученный результат меньше "0", то предприятие неэффективно работает в денежном выражении на полученный результат, чем среднее предприятие на данном конкурентном рынке.
Приведенная количественная оценка эффективности может быть дана не только по отношению средне эффективному, средне рискованному предприятию, но и по отношению к средне самому эффективному и мало рискованному. Или, наоборот, по отношению к самому неэффективному предприятию на данном рынке. Для этого необходимо дополнительно вычислить минимальный (kmin) и максимальный (kmax) коэффициент наклона регрессионного уравнения эталонной модели, тем самым, расширяя дискриминантный, кластерный анализ.
В алгоритме будем применять упрощенный, но достаточно точный расчет:
Для этого необходимо разделить каждый i-тый элемент вектора Y на i-тый элемент вектора X, т.е. ki=yi/xi.
В полученном векторе Y/Х найти минимальное значение kmin=Min(Y/Х).
В полученном векторе Y/Х найти максимальное значение kmax=Max(Y/Х).
Определить эффективность по отношению к средне лучшему предприятию на рынке Ymin= kmin*Xi - Yi.
Определить эффективность по отношению к средне худшему предприятию на рынке Ymax= kmax*Xi - Yi.
Следует отметить, что оценку эффективности по средне худшему предприятию проводить бессмысленно – зачем сравнивать исследуемый объект с заведомым "двоечником". Хотя и такой избыточный анализ, по нашему мнению, не сложен.